【伽羅瓦理論5】 

內容簡介

《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學中的美。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。

《數學女孩5：伽羅瓦理論》從鬼脚圖講起，結合二次方程式的求根公式、尺規作圖、群和域等知識，最終帶領讀者進入伽羅瓦理論的世界，還原伽羅瓦短暫的一生中璀璨不朽的數學成就。 整本書一氣呵成，非常適合對數學感興趣的初高中生以及成人閱讀。

作者簡介

結城浩（作者）

生於1963年，日本知名科技作家和程式師。 在程式設計語言、設計模式、數學、加密技術等領域，編寫了很多深受歡迎的入門書。 代表作有《數學女孩》系列、《程序員的數學》《圖解密碼技術》等。

陳冠貴（譯者）

專職日語譯者。 畢業於臺灣大學，修讀漢語、日語雙專業。 譯作橫跨文學、生活、經管、手工藝領域。 自我期許能悠遊於漢日語之間，帶給讀者閱讀無礙的文字饗宴。

目錄

序言

第1章有趣的鬼脚圖1

1.1交錯的鬼脚圖1

1.2溢出的鬼脚圖5

1.2.1計算數量5

1.2.2尤裡的疑問7

1.3理所當然的鬼脚圖8

1.3.1冰沙8

1.3.2無可替代之物8

1.3.3可以畫出鬼脚圖所有的排列模式嗎？ 9

1.4有趣的鬼脚圖14

1.4.1 3條分隔號14

1.4.2鬼脚圖的2次方16

1.4.3鬼脚圖的3次方18

1.4.4繪圖20

1.4.5解開深層謎題23

第2章睡美人的二次方程式25

2.1 2次方根25

2.1.1尤裡25

2.1.2負數 × 負數26

2.1.3複數平面27

2.2求根公式29

2.2.1二次方程式29

2.2.2方程式與多項式31

2.2.3推導二次方程式的求根公式32

2.2.4傳達心情36

2.3解與係數的關係37

2.3.1泰朵拉37

2.3.2解與係數的關係37

2.3.3整理思緒41

2.4對稱多項式與域的觀點42

2.4.1米爾嘉42

2.4.2再探解與係數的關係42

2.4.3再探求根公式49

2.4.4回家的路上56

第3章探索形式61

3.1正三角形61

3.1.1醫院61

3.1.2再次發燒70

3.1.3夢的結局71

3.2對稱群的形式73

3.2.1閱覽室73

3.2.2群公理74

3.2.3公理與定義83

3.3迴圈群的形式86

3.3.1前往“加庫拉”86

3.3.2結構86

3.3.3子群87

3.3.4基數91

3.3.5迴圈群92

3.3.6阿貝爾群95

第4章與你共軛101

4.1閱覽室101

4.1.1泰朵拉101

4.1.2因式分解102

4.1.3數的範圍104

4.1.4多項式的除法106

4.1.5 1的12次方根108

4.1.6正n邊形110

4.1.7三角函數111

4.1.8出路114

4.2迴圈群115

4.2.1米爾嘉115

4.2.2 12個複數116

4.2.3製作表格118

4.2.4共有頂點的正多邊形119

4.2.5 1的原始12次方根122

4.2.6分圓多項式124

4.2.7分圓方程式130

4.2.8與你共軛132

4.2.9迴圈群與生成元133

4.3模擬考試136

第5章角的三等分139

5.1圖的世界139

5.1.1尤裡139

5.1.2角的三等分問題140

5.1.3對於“角的三等分”問題的誤解144

5.1.4尺子與圓規145

5.1.5可以作圖的意義147

5.2數的世界148

5.2.1具體例子148

5.2.2通過作圖實現加減乘除運算151

5.2.3通過作圖開根號154

5.3三角函數的世界158

5.3.1雙倉圖書館158

5.3.2理紗159

5.3.3離別之際163

5.4方程式的世界164

5.4.1看穿結構164

5.4.2用有理數練習169

5.4.3一步的重複172

5.4.4能進入下一個步驟嗎？ 173

5.4.5發現了嗎？ 176

5.4.6預測與定理178

5.4.7出路在哪裡？ 180

第6章支撐天空之物187

6.1維度187

6.1.1廟會187

6.1.2四維世界188

6.1.3章魚燒190

6.1.4支撐之物192

6.2線性空間194

6.2.1閱覽室194

6.2.2座標平面196

6.2.3線性空間199

6.2.4 R上的線性空間C 202

6.2.5 Q上的線性空間Q（√2）203

6.2.6擴張的程度208

6.3線性獨立212

6.3.1線性獨立212

6.3.2維度的不變性216

6.3.3擴張次數217

第7章拉格朗日預解式的秘密221

7.1三次方程式的求根公式221

7.1.1泰朵拉221

7.1.2紅色卡片：契爾恩豪森轉換222

7.1.3橙色卡片：解與係數的關係225

7.1.4黃色卡片：拉格朗日預解式227

7.1.5綠色卡片：3次方的和231

7.1.6藍色卡片：3次方的積236

7.1.7靛色的卡片：從係數到解238

7.1.8紫色卡片：三次方程式的求根公式243

7.1.9描繪“旅行地圖”244

7.2拉格朗日預解式248

7.2.1米爾嘉248

7.2.2拉格朗日預解式的性質253

7.2.3能應用於其他例子嗎？ 257

7.3二次方程式的求根公式258

7.3.1二次方程式的拉格朗日預解式258

7.3.2判別式261

7.4五次方程式的求根公式263

7.4.1五次方程式是什麼263

7.4.2“五”的意義264

第8章建造塔267

8.1音樂267

8.1.1咖啡廳267

8.1.2邂逅269

8.2講課270

8.2.1閱覽室270

8.2.2擴張次數270

8.2.3擴域與子域271

8.2.4 Q（√2）/Q 273

8.2.5出題275

8.2.6 Q（√2，√3）/Q 276

8.2.7擴張次數的積279

8.2.8（Q（√2+√3）/Q）282

8.2.9最小多項式284

8.2.10新發現？ 288

8.3信293

8.3.1歸途293

8.3.2家294

8.3.3信295

8.3.4規矩數295

8.3.5晚餐297

8.3.6朝著方程式的可解性前進298

8.3.7最小分裂域300

8.3.8正規擴張300

8.3.9面對真實的對象303

第9章心情的形式307

9.1對稱群S3的形式307

9.1.1雙倉圖書館307

9.1.2類別313

9.1.3陪集317

9.1.4整齊的形式319

9.1.5製作群322

9.2寫法的形式329

9.2.1 Oxygen 329

9.2.2置換的寫法330

9.2.3拉格朗日定理332

9.2.4正規子群的寫法337

9.3部分的形式337

9.3.1孤零零的2 337

9.3.2探索結構338

9.3.3伽羅瓦的正規分解339

9.3.4進一步除以C3 340

9.3.5除法與同等看待344

9.4對稱群S4的形式348

9.5心情的形式351

9.5.1 Iodine 351

9.5.2熄燈時間352

第10章伽羅瓦理論355

10.1伽羅瓦節355

10.1.1簡略年表355

10.1.2第一論文358

10.2定義361

10.2.1定義（可約與既約）361

10.2.2定義（置換群）364

10.2.3兩個世界366

10.3引理367

10.3.1引理1（既約多項式的性質）367

10.3.2引理2（用根製作的V）370

10.3.3引理3（用V表示根）372

10.3.4引理4（V的共軛）374

10.4定理378

10.4.1定理1（“方程式的伽羅瓦群”的定義）378

10.4.2方程式x2 3x + 2 = 0的伽羅瓦群380

10.4.3方程式ax2 + bx + c = 0的伽羅瓦群382

10.4.4伽羅瓦群的製作方法387

10.4.5方程式x3 2x = 0的伽羅瓦群390

10.4.6定理2（縮小方程式的“伽羅瓦群”）394

10.4.7伽羅瓦的錯誤398

10.4.8定理3（添加輔助方程式的所有的根）399

10.4.9重複縮小401

10.4.10定理4（縮小的伽羅瓦群的性質）403

10.5定理5（以代數管道解方程式的充分必要條件）404

10.5.1伽羅瓦提出的問題404

10.5.2何謂“以代數管道解方程式”407

10.5.3泰朵拉的問題408

10.5.4 p次方根的添加409

10.5.5伽羅瓦的添加元素413

10.5.6手忙腳亂的尤裡418

10.6兩座塔418

10.6.1三次方程式的一般形式418

10.6.2四次方程式的一般形式420

10.6.3二次方程式的一般形式424

10.6.4五次方程式不存在求根公式426

10.7夏天結束428

10.7.1伽羅瓦理論的基本定理428

10.7.2展覽432

10.7.3夜晚的Oxygen 432

10.7.4無可替代之物434

尾聲437

後記444

參考文獻和導讀447

書摘插畫

-----------------------------------------------------------------------------------

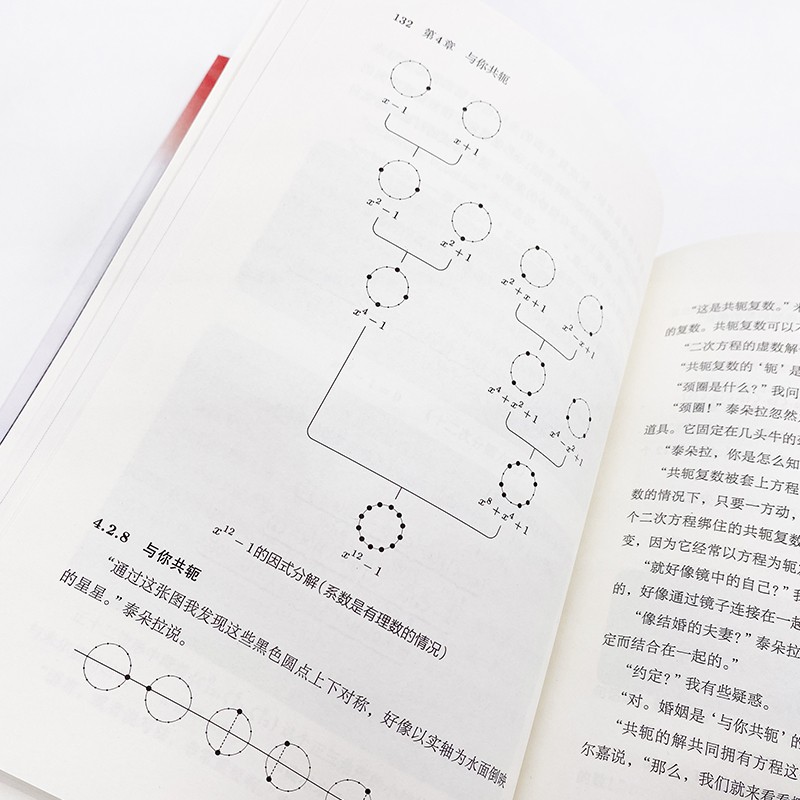
 【龐加萊猜想】 

內容簡介

《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學之美的過程。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。 《數學女孩6：龐加萊猜想》以百年數學難題“龐加萊猜想”為主題，從柯斯堡七橋問題入手，詳細講解了拓撲學、非歐幾何、流形、微分方程、高斯絕妙定理和傅立葉展開式等數學知識，還原了龐加萊猜想的探索歷程，帶領讀者一同追尋“宇宙的形狀”。 整本書一氣呵成，非常適合對數學感興趣的初高中生以及成人閱讀。 請翻開本書，一同加入主人公們的探索之旅吧。

作者簡介

結城浩（作者）

生於1963年，日本科技作家和程式師。 在程式設計語言、設計模式、數學、加密技術等領域，編寫了很多深受歡迎的入門書。 代表作有《數學女孩》系列、《程序員的數學》《圖解密碼技術》等。

陳朕疆（譯者）

自由譯者，曾在日本京都大學交換留學一年。

目錄

序言

第1章柯尼斯堡七橋問題1

1.1尤裡1

1.2一筆劃問題2

1.3從簡單的圖開始7

1.4圖與次數11

1.5這也是數學嗎15

1.6逆定理的證明18

第2章默比烏斯帶和克萊因瓶35

2.1樓頂35

2.1.1泰朵拉35

2.1.2默比烏斯帶36

2.2教室39

2.3圖書室40

2.3.1米爾嘉40

2.3.2分類43

2.3.3閉曲面的分類45

2.3.4可定向曲面46

2.3.5不可定向曲面49

2.3.6展開圖51

2.3.7連通和63

2.4歸途72

第3章泰朵拉的身邊75

3.1家人的身邊75

3.2 0的附近77

3.2.1練習77

3.2.2全等與相似81

3.2.3對應關係84

3.3實數a的附近86

3.3.1全等、相似、同胚86

3.3.2連續函數88

3.4點a的附近94

3.4.1前往异世界的準備94

3.4.2距離的世界：實數a的 δ  鄰域95

3.4.3距離的世界：開集96

3.4.4距離的世界：開集的性質98

3.4.5旅程：從距離的世界到拓撲的世界101

3.4.6拓撲的世界：開集公理103

3.4.7拓撲的世界：開鄰域106

3.4.8拓撲的世界：連續映射108

3.4.9同胚映射115

3.4.10不變性116

3.5泰朵拉的身邊117

第4章非歐幾何123

4.1球面幾何123

4.2現在和未來之間130

4.3雙曲幾何131

4.3.1所謂的“學習”131

4.3.2非歐幾何132

4.3.3鮑耶與羅巴切夫斯基137

4.3.4自己家141

4.4跳出畢氏定理142

4.4.1理紗142

4.4.2距離的定義143

4.4.3龐加萊圓盤模型145

4.4.4半平面模型152

4.5超越平行公理153

4.6自己家156

第5章跳入流形159

5.1跳出日常159

5.1.1輪到我了159

5.1.2為了打倒惡龍160

5.1.3尤裡的疑問161

5.1.4考慮低維的情况162

5.1.5會歪成什麼樣子呢168

5.2跳入非日常174

5.2.1櫻花樹下174

5.2.2內外翻轉175

5.2.3展開圖177

5.2.4龐加萊猜想182

5.2.5二維球面183

5.2.6三維球面185

5.3要跳入，還是跳出187

5.3.1醒過來時187

5.3.2 Eulerians 188

第6章捕捉看不到的形狀193

6.1捕捉形狀193

6.1.1沉默的形狀193

6.1.2問題的形狀195

6.1.3發現197

6.2用群來捕捉形狀199

6.2.1以數為線索199

6.2.2線索是什麼204

6.3用自環來捕捉形狀206

6.3.1自環206

6.3.2自環上的同倫210

6.3.3同倫類213

6.3.4同倫群216

6.4掌握球面218

6.4.1自己家218

6.4.2一維球面的基本群218

6.4.3二維球面的基本群219

6.4.4三維球面的基本群221

6.4.5龐加萊猜想221

6.5被限制的形狀223

6.5.1確認條件223

6.5.2捕捉我所不知道的自己225

第7章微分方程的溫度229

7.1微分方程229

7.1.1音樂教室229

7.1.2教室231

7.1.3指數函數236

7.1.4三角函數243

7.1.5微分方程的目的245

7.1.6彈簧振動247

7.2牛頓冷卻定律253

第8章高斯絕妙定理263

8.1車站前263

8.1.1尤裡263

8.1.2讓人驚訝的事267

8.2自己家268

8.2.1媽媽268

8.2.2罕有之物271

8.3圖書室272

8.3.1泰朵拉272

8.3.2理所當然的事275

8.4加庫拉277

8.4.1米爾嘉277

8.4.2傾聽277

8.4.3解題279

8.4.4高斯曲率283

8.4.5絕妙定理286

8.4.6齊性和各向同性288

8.4.7回禮289

第9章靈感與毅力291

9.1三角函數訓練291

9.1.1靈感與毅力291

9.1.2組織圓292

9.1.3正弦曲線296

9.1.4從旋轉矩陣到兩角和公式297

9.1.5從兩角和公式到積化和差公式298

9.1.6媽媽300

9.2合格判定模擬考302

9.2.1不要緊張302

9.2.2不要被騙302

9.2.3需要靈感還是毅力305

9.3看穿算式的形式311

9.3.1概率密度函數的研究311

9.3.2拉普拉斯積分的研究317

9.4傅立葉展開式322

9.4.1靈感322

9.4.2傅立葉展開式324

9.4.3超越毅力329

9.4.4超越靈感331

第10章龐加萊猜想335

10.1公開研討會335

10.1.1課程結束之後335

10.1.2午餐時間336

10.2龐加萊337

10.2.1形狀337

10.2.2龐加萊猜想339

10.2.3瑟斯頓的幾何化猜想343

10.2.4哈密頓的裡奇流方程345

10.3數學家們346

10.3.1年表346

10.3.2菲爾茲獎348

10.3.3千禧年大獎難題350

10.4哈密頓352

10.4.1裡奇流方程式352

10.4.2傅立葉的熱傳導方程353

10.4.3顛覆性的想法354

10.4.4哈密頓計畫356

10.5佩雷爾曼359

10.5.1佩雷爾曼的論文359

10.5.2再前進一步362

10.6傅立葉363

10.6.1傅立葉的時代363

10.6.2熱傳導方程364

10.6.3分離變數法368

10.6.4重疊積分370

10.6.5傅立葉積分371

10.6.6觀察類似的式子375

10.6.7回到裡奇流方程376

10.7我們377

10.7.1從過去到未來377

10.7.2冬天來了378

10.7.3春天不遠了379

尾聲381

後記385

參考文獻和導讀389

書摘插畫

-----------------------------------------------------------------------------------

【數學女孩】

內容簡介

《數學女孩》以小說的形式展開，重點描述一群年輕人探尋數學中的美。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的初等數學科普書”。 內容涉及數列和數學模型、斐波那契數列、卷積、調和數、泰勒展開、巴塞爾問題、分拆數等，非常適合對數學感興趣的初高中生以及成人閱讀。

作者簡介

結城浩（作者）

日本科技作家和程式師。 二十年來筆耕不輟，在程式設計語言、設計模式、數學、密碼技術等領域，編寫著作三十餘本。 代表作有《數學女孩》系列、《程序員的數學》等。

作者主頁： http://www.hyuki.com/

朱一飛（譯者）

復旦大學日語系碩士，曾獲日本文部省獎學金赴日本早稻田大學、關西大學交換留學。 現任復旦大學外事處項目官員、復旦大學日本研究中心兼職研究員，譯有《小王金魚生活》《只要一分鐘》《情路9號》《斷食法》《猫叔來了》《新娘修煉記》等。

目錄

致讀者1

序言1

第1章數列和數學模型1

1.1櫻花樹下1

1.2自己家5

1.3數列智力題沒有正確答案8

第2章一封名叫數學公式的情書13

2.1在校門口13

2.2心算智力題14

2.3信15

2.4放學後16

2.5階梯教室17

2.5.1質數的定義19

2.5.2值的定義23

2.6回家路上25

2.7自己家27

2.8米爾嘉的解答31

2.9圖書室33

2.9.1方程式和恒等式33

2.9.2積的形式與和的形式37

2.10在數學公式另一頭的人到底是誰41

第3章 ω 的華爾滋43

3.1圖書室43

3.2振動和旋轉46

3.3 ω  53

第4章斐波那契數列和生成函數61

4.1圖書室61

4.1.1找規律62

4.1.2等比數列的和64

4.1.3向無窮級數進軍64

4.1.4向生成函數進軍66

4.2抓住斐波那契數列的關鍵68

4.2.1斐波那契數列68

4.2.2斐波那契數列的生成函數70

4.2.3封閉運算式71

4.2.4用無窮級數來表示73

4.2.5解决75

4.3回顧79

第5章基本不等式81

5.1在“神樂”81

5.2滿是疑問83

5.3不等式85

5.4再進一步看看94

5.5關於學習97

第6章在米爾嘉旁邊103

6.1微分103

6.2差分107

6.3微分和差分109

6.3.1一次函數x 110

6.3.2二次函數x2 111

6.3.3三次函數x3 113

6.3.4指數函數e x 115

6.4在兩個世界中往返的旅行117

第7章卷積121

7.1圖書室121

7.1.1米爾嘉121

7.1.2泰朵拉125

7.1.3推導公式125

7.2在回家路上談一般化129

7.3在咖啡店談二項式定理130

7.4在自己家裡解生成函數140

7.5圖書室146

7.5.1米爾嘉的解146

7.5.2研究生成函數152

7.5.3圍巾155

7.5.4 **後的要塞156

7.5.5攻陷159

7.5.6半徑是0的圓163

第8章調和數167

8.1尋寶167

8.1.1泰朵拉167

8.1.2米爾嘉169

8.2圖書室裏的對話170

8.2.1部分和與無窮級數170

8.2.2從理所當然的地方開始173

8.2.3命題175

8.2.4對於所有的……178

8.2.5存在……180

8.3螺旋式樓梯的音樂教室184

8.4令人掃興的函數186

8.5對無窮大的過高評估187

8.6在教室中研究調和函數194

8.7兩個世界、四種運算197

8.8已知的鑰匙、未知的門203

8.9如果世界上只有兩個質數205

8.9.1卷積206

8.9.2收斂的等比數列207

8.9.3質因數分解的定理208

8.9.4質數無限性的證明209

8.10天象儀213

第9章泰勒展開和巴塞爾問題217

9.1圖書室217

9.1.1兩張卡片217

9.1.2無限次多項式219

9.2自學222

9.3在那家叫“豆子”的咖啡店224

9.3.1微分的規則224

9.3.2更進一步微分227

9.3.3 sin x的泰勒展開230

9.3.4極限函數的影像233

9.4自己家237

9.5代數學基本定理239

9.6圖書室245

9.6.1泰朵拉的嘗試245

9.6.2要到達哪裡248

9.6.3向無限挑戰255

第10章分拆數259

10.1圖書室259

10.1.1分拆數259

10.1.2舉例261

10.2回家路上267

10.2.1斐波那契手勢267

10.2.2分組269

10.3“豆子”咖啡店271

10.4自己家273

10.5音樂教室278

10.5.1我的發言（分拆數的生成函數）279

10.5.2米爾嘉的發言（分拆數的上限）287

10.5.3泰朵拉的發言292

10.6教室296

10.7尋找更好的上限之旅298

10.7.1以生成函數為出發點299

10.7.2“第一個轉角”積變為和300

10.7.3“東邊的森林”泰勒展開301

10.7.4“西邊的山丘”調和數307

10.7.5旅行結束308

10.7.6泰朵拉的回顧311

10.8明天見312

尾聲315

結語319

參考文獻和導讀321

-----------------------------------------------------------------------------------

【費馬大定理】

內容簡介

《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學中的美。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。

《數學女孩2：費馬大定理》有許多巧思。 每一章針對不同議題進行解說，再於末尾一章切入正題——費馬大定理。 作者巧妙地以每一章的概念作為拼圖，拼出被稱為“世紀謎題”的費馬大定理的大概證明。 整本書一氣呵成，非常適合對數學感興趣的初高中生以及成人閱讀。

作者簡介

結城浩

日本科技作家和程式師。 二十年來筆耕不輟，在程式設計語言、設計模式、數學、密碼技術等領域，編寫著作三十餘本。 代表作有《數學女孩》系列、《程序員的數學》等。

目錄

序言1

第1章將無限宇宙盡收掌心1

1.1銀河1

1.2發現2

1.3找不同3

1.4時鐘巡迴6

1.5完全巡迴的條件13

1.6巡迴哪裡15

1.7超越人類的極限19

1.8是什麼東西，你們知道嗎22

第2章畢氏定理25

2.1泰朵拉25

2.2米爾嘉29

2.3尤裡32

2.4畢達哥拉·榨汁機33

2.5家中35

2.5.1調查奇偶性35

2.5.2使用數學公式37

2.5.3向著乘積的形式進發38

2.5.4互質40

2.5.5分解質因數43

2.6給泰朵拉講解49

2.7十分感謝51

2.8組織圓上的有理點52

第3章互質59

3.1尤裡59

3.2分數61

3.3 **大公約數和**小公倍數63

3.4打破砂鍋問到底的人68

3.5米爾嘉69

3.6質數指數記數法70

3.6.1實例70

3.6.2節奏加快73

3.6.3乘法運算74

3.6.4 **大公約數75

3.6.5向著無限維空間出發77

3.7米爾嘉大人78

第4章反證法83

4.1家中83

4.1.1定義83

4.1.2命題86

4.1.3數學公式88

4.1.4證明95

4.2高中97

4.2.1奇偶97

4.2.2衝突101

第5章可以粉碎的質數105

5.1教室105

5.1.1速度題105

5.1.2用一次方程定義數位107

5.1.3用二次方程定義數位109

5.2複數的和與積111

5.2.1複數的和111

5.2.2複數的積112

5.2.3複平面上的±i 116

5.3五個格點120

5.3.1卡片120

5.3.2“豆子”咖啡店122

5.4可以粉碎的質數126

第6章阿貝爾群的眼淚141

6.1奔跑的早晨141

6.2 144

6.2.1為了將運算引入集合144

6.2.2運算145

6.2.3結合律148

6.2.4組織元149

6.2.5逆元150

6.2.6群的定義151

6.2.7群的示例151

6.2.8 **小的群155

6.2.9有2個元素的群156

6.2.10同構158

6.2.11用餐160

6.3第二天160

6.3.1交換律160

6.3.2正多邊形162

6.3.3數學文章的解釋164

6.3.4辯群公理166

6.4真實的樣子167

6.4.1本質和抽象化167

6.4.2搖擺不定的心169

第7章以髮型為模173

7.1時鐘173

7.1.1餘數的定義173

7.1.2時針訓示之物176

7.2同餘177

7.2.1餘項177

7.2.2同餘181

7.2.3同餘的含義184

7.2.4不拘小節地同等看待184

7.2.5等式和同餘式185

7.2.6兩邊同時做除法運算的條件186

7.2.7拐杖190

7.3除法的本質192

7.3.1喝著可哥192

7.3.2運算錶的研究193

7.3.3證明198

7.4群·環·域200

7.4.1既約剩餘類群200

7.4.2由群到環203

7.4.3由環到域209

7.5以髮型為模214

第8章無窮遞降法217

8.1費馬大定理217

8.2泰朵拉的三角形224

8.2.1圖書室224

8.2.2曲曲折折的小路229

8.3我的旅行230

8.3.1旅行的出發點：用m，n表示A，B，C，D 230

8.3.2原子和基本粒子的關係：用e，f，s，t表示m，n 235

8.3.3研究基本粒子s+t，s-t 237

8.3.4基本粒子和誇克的關係：用u，v表示s，t 240

8.4尤裡的靈感242

8.4.1房間242

8.4.2小學243

8.4.3自動販賣機245

8.5米爾嘉的證明252

8.5.1備戰252

8.5.2米爾嘉253

8.5.3就差填上**後一塊拼圖258

第9章**美的數學公式261

9.1 **美的數學公式261

9.1.1歐拉的式子261

9.1.2歐拉的公式263

9.1.3指數運算法則267

9.1.4 -1次方，1/2次方272

9.1.5指數函數273

9.1.6遵守數學公式277

9.1.7向三角函數架起橋樑279

9.2準備慶功宴286

9.2.1音樂教室286

9.2.2自己家287

第10章費馬大定理289

10.1公開研討會289

10.2歷史291

10.2.1問題291

10.2.2初等數論的時代292

10.2.3代數數論時代293

10.2.4幾何數論時代295

10.3懷爾斯的興奮296

10.3.1搭乘時間機器296

10.3.2從“1986年的景色”發現問題297

10.3.3半穩定的橢圓曲線300

10.3.4證明概要302

10.4橢圓曲線的世界303

10.4.1什麼是橢圓曲線303

10.4.2從有理數域到有限域305

10.4.3有限域F 307

10.4.4有限域F 309

10.4.5有限域F 5 310

10.4.6點的個數312

10.4.7棱柱313

10.5自守形式的世界314

10.5.1保護形式314

10.5.2 q展開316

10.5.3從F（q）到數列a（k）317

10.6穀山-志村定理321

10.6.1兩個世界321

10.6.2弗賴曲線323

10.6.3半穩定323

10.7慶功宴326

10.7.1自己家中326

10.7.2 Zeta·變奏曲327

10.7.3生產的孤獨330

10.7.4尤裡的靈感331

10.7.5並非偶然334

10.7.6平安夜336

10.8仙女座也研究數學336

尾聲341

後記345

參考文獻和導讀347

-----------------------------------------------------------------------------------

【哥德爾不完備定理3】 

內容簡介

《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學中的美。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。

《數學女孩3：哥德爾不完備定理》有許多巧思。 每一章針對不同議題進行解說，再於**後一章切入正題——哥德爾不完備定理。 作者巧妙地以每一章的概念作為拼圖，拼出與塔斯基的形式語言的真理論、圖靈機和判定問題一道被譽為“現代邏輯科學在哲學方面的三大成果”的哥德爾不完備定理的大概證明。 整本書一氣呵成，非常適合對數學感興趣的初高中生以及成人閱讀。

作者簡介

結城浩

生於1963年。 日本知名科技作家和程式師。 在程式設計語言、設計模式、數學、加密技術等領域，編寫了很多深受歡迎的入門書。 代表作有《數學女孩》系列、《程序員的數學》、《圖解密碼技術》等。

目錄

序言

第1章鏡子的獨白1

1.1誰是老實人.1

1.1.1鏡子呀鏡子.1

1.1.2誰是老實人.3

1.1.3相同的回答.7

1.1.4回答是沉默.8

1.2邏輯謎題.9

1.2.1愛麗絲、博麗絲和克麗絲.9

1.2.2用表格來想10

1.2.3出題者的心思14

1.3帽子是什麼顏色15

1.3.1不知道15

1.3.2對出題者的驗證18

1.3.3鏡子的獨白19

第2章皮亞諾算術23

2.1泰朵拉23

2.1.1皮亞諾公理23

2.1.2無數個願望27

2.1.3皮亞諾公理.PA1.28

2.1.4皮亞諾公理.PA2.29

2.1.5養大32

2.1.6皮亞諾公理PA3.34

2.1.7小的？ 35

2.1.8皮亞諾公理.PA4.36

2.2米爾嘉39

2.2.1皮亞諾公理PA5.42

2.2.2數學歸納法43

2.3在無數脚步之中49

2.3.1有限？ 無限？ 49

2.3.2動態？ 靜態？ 50

2.4尤裡52

2.4.1加法運算？ 52

2.4.2公理呢？ 53

第3章伽利略的猶豫57

3.1集合57

3.1.1美人的集合57

3.1.2外延標記法58

3.1.3餐桌60

3.1.4空集61

3.1.5集合的集合62

3.1.6公共部分64

3.1.7並集67

3.1.8包含關係68

3.1.9為什麼要研究集合71

3.2邏輯72

3.2.1內涵標記法72

3.2.2羅素悖論74

3.2.3集合運算和邏輯運算77

3.3無限79

3.3.1雙射鳥籠79

3.3.2伽利略的猶豫83

3.4表示86

3.4.1歸途86

3.4.2書店87

3.5沉默88

第4章無限接近的目的地91

4.1家中91

4.1.1尤裡91

4.1.2男生的“證明”92

4.1.3尤裡的“證明”93

4.1.4尤裡的“疑惑”96

4.1.5我的講解97

4.2量販店99

4.3音樂教室104

4.3.1字母的導入104

4.3.2極限106

4.3.3憑聲音决定音樂108

4.3.4極限的計算111

4.4歸途119

第5章萊布尼茨之夢123

5.1若尤裡，則非泰朵拉123

5.1.1“若……則……”的含義123

5.1.2萊布尼茨之夢126

5.1.3理性的界限？ 128

5.2若泰朵拉，則非尤裡129

5.2.1備戰高考129

5.2.2上課131

5.3若米爾嘉，則米爾嘉133

5.3.1教室133

5.3.2形式系統135

5.3.3邏輯公式137

5.3.4“若……則……”的形式140

5.3.5公理142

5.3.6證明論143

5.3.7推理規則145

5.3.8證明和定理147

5.4不是我，還是我149

5.4.1家中149

5.4.2形式的形式150

5.4.3含義的含義152

5.4.4若“若……則……”，則……153

5.4.5邀約157

第6章- δ 語言159

6.1數列的極限159

6.1.1從圖書室出發159

6.1.2到達階梯教室160

6.1.3理解複雜式子的方法164

6.1.4看絕** 166

6.1.5看“若……則……”169

6.1.6看“所有”和“某個”170

6.2函數的極限174

6.2.1- δ  174

6.2.2- δ 的含義177

6.3摸底考試178

6.3.1上榜178

6.3.2靜寂的聲音、沉默的聲音179

6.4“連續”的定義181

6.4.1圖書室181

6.4.2在所有點處都不連續184

6.4.3是否存在在一點處連續的函數186

6.4.4逃出無限的迷宮187

6.4.5在一點處連續的函數！ 188

6.4.6訴衷腸192

第7章對角論證法197

7.1數列的數列197

7.1.1可數集197

7.1.2對角論證法201

7.1.3挑戰：給實數編號209

7.1.4挑戰：有理數和對角論證法213

7.2形式系統的形式系統215

7.2.1相容性和完備性215

7.2.2哥德爾不完備定理222

7.2.3算術224

7.2.4形式系統的形式系統225

7.2.5詞彙的整理229

7.2.6數項229

7.2.7對角化230

7.2.8數學的定理232

7.3失物的失物233

第8章兩份孤獨所衍生的產物239

8.1重疊的對239

8.1.1泰朵拉的發現239

8.1.2我的發現245

8.1.3誰都沒發現的事實246

8.2家中247

8.2.1自己的數學247

8.2.2表現的壓縮247

8.2.3加法運算的定義251

8.2.4教師的存在254

8.3等價關係255

8.3.1畢業典禮255

8.3.2對衍生的產物257

8.3.3從自然數到整數258

8.3.4圖259

8.3.5等價關係264

8.3.6商集268

8.4餐廳272

8.4.1兩個人的晚飯272

8.4.2一對翅膀272

8.4.3無力考試275

第9章令人迷惑的螺旋樓梯277

9.1π弧度277

9.1.1不高興的尤裡277

9.1.2三角函數279

9.1.3 sin45°282

9.1.4 sin60°286

9.1.5正弦曲線290

9.2π弧度294

9.2.1弧度294

9.2.2教人296

9.3π弧度297

9.3.1停課297

9.3.2餘數298

9.3.3燈塔300

9.3.4海邊303

9.3.5消毒304

第10章哥德爾不完備定理307

10.1雙倉圖書館307

10.1.1入口307

10.1.2氯308

10.2希爾伯特計畫310

10.2.1希爾伯特310

10.2.2猜謎312

10.3哥德爾不完備定理316

10.3.1哥德爾316

10.3.2討論318

10.3.3證明的概要320

10.4春天—形式系統P.320

10.4.1基本符號320

10.4.2數項和符號322

10.4.3邏輯公式323

10.4.4公理324

10.4.5推理規則327

10.5午飯時間328

10.5.1元數學328

10.5.2用數學研究數學329

10.5.3蘇醒329

10.6夏天—哥德爾數331

10.6.1基本符號的哥德爾數331

10.6.2序列的哥德爾數332

10.7秋天—原始遞迴性335

10.7.1原始遞迴函數335

10.7.2原始遞迴函數（謂詞）的性質338

10.7.3表現定理340

10.8冬天—通往可證明性的漫長之旅343

10.8.1整理行裝343

10.8.2數論344

10.8.3序列346

10.8.4變數·符號·邏輯公式348

10.8.5公理、定理、形式證明358

10.9新春—不可判定語句362

10.9.1“季節”的確認362

10.9.2種子—從含義的世界到形式的世界364

10.9.3綠芽—p的定義366

10.9.4枝杈—r的定義367

10.9.5葉子—從A1往下走368

10.9.6蓓蕾—從B1開始往下走369

10.9.7不可判定語句的定義369

10.9.8梅花—.IsProvable（g）.370

10.9.9桃花—.IsProvable（not（g））的證明372

10.9.10櫻花—證明形式系統P是不完備的374

10.10不完備定理的意義376

10.10.1“‘我’是無法證明的”376

10.10.2第二不完備定理的證明之概要380

10.10.3不完備定理衍生的產物383

10.10.4數學的界限？ 384

10.11帶上夢想386

10.11.1並非結束386

10.11.2屬於我387

尾聲391

後記395

參考文獻和導讀399

-----------------------------------------------------------------------------------

【隨機算灋4】 

內容簡介

《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學中的美。 內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。

《數學女孩4：隨機算法》以“隨機算灋”為主題，從純粹的數學和電腦程式設計兩個角度對隨機算灋進行了細緻的講解。 內容涉及排列組合、概率、期望、線性法則、矩陣、順序查找算灋、二分查找算灋、冒泡排序算灋和快速排序算灋等。 整本書一氣呵成，非常適合對數學和算灋感興趣的初高中生以及成人閱讀。

作者簡介

結城浩（作者）

生於1963年，日本知名科技作家和程式師。 在程式設計語言、設計模式、數學、加密技術等領域，編寫了很多深受歡迎的入門書。 代表作有《數學女孩》系列、《程序員的數學》《圖解密碼技術》等。

作者主頁： http://www.hyuki.com

叢熙（譯者）

2017年本科畢業於東北大學機械系，現於日本奈良先端科學技術大學院大學攻讀碩士學位，研究方向為增強現實。

江志强（譯者）

電腦應用軟體工程師，畢業於廈門大學數學專業，現時在民航空管行業從事通信導航工作。 業餘時間沉迷於數學與算灋。

目錄

序言

第1章絕不會輸的賭博1

1.1擲骰子1

1.2拋硬幣4

1.2.1兩枚硬幣4

1.2.2一枚硬幣7

1.2.3彩票的記憶8

1.3蒙提霍爾問題11

1.3.1 3個信封11

1.3.2上帝視角18

第2章積跬步，致千里21

2.1高中21

2.1.1泰朵拉21

2.1.2理紗22

2.1.3順序查找24

2.1.4逐行調試28

2.1.5順序查找演算法分析34

2.1.6順序查找演算法分析（能找到v的情况）35

2.1.7順序查找演算法分析（無法找到v的情况）38

2.2演算法分析40

2.2.1米爾嘉40

2.2.2演算法分析41

2.2.3不同情况的歸納42

2.2.4思考意義45

2.2.5帶有哨兵的順序查找算灋48

2.2.6創造歷史52

2.3自己家54

第3章171億7986萬9184份孤獨61

3.1排列61

3.1.1書店61

3.1.2豁然開朗62

3.1.3具體示例63

3.1.4找規律65

3.1.5一般化70

3.1.6鋪就道路72

3.1.7那傢伙74

3.2組合76

3.2.1圖書室76

3.2.2排列77

3.2.3組合79

3.2.4鱺魚與綠鯉魚82

3.2.5二項式定理83

3.3 2n的分配88

3.3.1帕斯卡三角形88

3.3.2比特模式92

3.3.3指數爆炸94

3.4幂運算的孤獨96

3.4.1回家路上96

3.4.2家96

第4章可能性中的不確定性99

4.1可能性中的確定性99

4.2可能性中的不確定性106

4.2.1相同的可能性106

4.2.2真正的武器107

4.3可能性的實驗109

4.3.1解釋程式109

4.3.2擲骰子比賽112

4.3.3輪盤比賽113

4.4可能性的倒塌115

4.4.1概率的定義115

4.4.2概率的意義118

4.4.3數學的應用118

4.4.4解答疑問120

4.5可能性的公理定義121

4.5.1柯爾莫哥洛夫121

4.5.2樣本空間與概率分佈函數121

4.5.3概率公理125

4.5.4子集與事件126

4.5.5概率公理P1 129

4.5.6概率公理P2 130

4.5.7概率公理P3 131

4.5.8還沒有明白132

4.5.9擲出的點數為偶數的概率134

4.5.10質地不均勻的骰子和豎立的硬幣137

4.5.11約定138

4.5.12咳嗽139

第5章期望143

5.1隨機變數143

5.1.1媽媽143

5.1.2泰朵拉144

5.1.3隨機變數的示例146

5.1.4概率分佈函數的示例150

5.1.5許多詞152

5.1.6期望153

5.1.7公平的遊戲157

5.2線性法則159

5.2.1米爾嘉159

5.2.2和的期望等於期望的和160

5.3二項分佈165

5.3.1硬幣的話題165

5.3.2二項分佈的期望168

5.3.3劃分為和的形式171

5.3.4指示器隨機變數172

5.3.5快樂的工作174

5.4直到所有事情發生175

5.4.1不知何時175

5.4.2能盡全力嗎176

5.4.3運用學到的知識180

5.4.4盡全力183

5.4.5意料之外的事情192

第6章難以捉摸的未來197

6.1約定的記憶197

6.2階199

6.2.1更快的算灋199

6.2.2至多為n階201

6.2.3出題204

6.2.4至多為f（n）階206

6.2.5 log n 211

6.3查找215

6.3.1二分查找215

6.3.2實例217

6.3.3分析220

6.3.4前往排序227

6.4排序228

6.4.1冒泡排序228

6.4.2實例229

6.4.3分析231

6.4.4大O標記法的層級235

6.5動態視角、靜態視角237

6.5.1需要比較多少次呢237

6.5.2比較樹239

6.5.3 log n！ 的評估241

6.6傳遞和學習245

6.6.1傳遞245

6.6.2學習246

第7章矩陣249

7.1圖書室249

7.1.1瑞穀老師249

7.1.2 TETRALIANE 250

7.2尤裡252

7.2.1無解252

7.2.2無窮多解254

7.2.3唯一解256

7.2.4信268

7.3泰朵拉269

7.3.1圖書室269

7.3.2行與列269

7.3.3矩陣與向量的積271

7.3.4聯立方程式與矩陣273

7.3.5矩陣的積274

7.3.6逆矩陣275

7.4米爾嘉280

7.4.1看穿隱藏的謎題280

7.4.2線性變換286

7.4.3旋轉293

7.5回家路上296

第8章孤零零的隨機漫步301

8.1家301

8.1.1雨天的週六301

8.1.2下午茶時間302

8.1.3鋼琴問題302

8.1.4旋律示例305

8.1.5解題方法一：毅力比拼308

8.1.6解題方法二：一招定勝負310

8.1.7一般化314

8.1.8搖擺不定的心319

8.2清晨的上學路320

8.3中午的教室322

8.3.1矩陣的練習322

8.3.2搖擺不定的心325

8.4放學後的圖書室327

8.4.1流浪問題327

8.4.2 A2的意義331

8.4.3向著矩陣的n次方前進332

8.4.4上半場準備：對角矩陣333

8.4.5下半場準備：矩陣與逆矩陣的三明治335

8.4.6向著特徵值前進336

8.4.7向著特徵向量前進342

8.4.8求An 344

8.5家347

8.5.1搖擺不定的心347

8.5.2雨夜349

第9章堅強、正直、美麗351

9.1家351

9.2圖書室358

9.2.1邏輯題358

9.2.2可滿足性問題358

9.2.3 3-SAT 360

9.2.4滿足363

9.2.5分配管道的練習364

9.2.6 NP完全問題365

9.3回家路上367

9.3.1誓言與約定367

9.3.2會議368

9.4圖書室369

9.4.1求解3-SAT問題的隨機算灋369

9.4.2隨機漫步371

9.4.3向著定量評估前進376

9.4.4另一個隨機漫步378

9.4.5關注迴圈379

9.5家384

9.5.1幸運的評估384

9.5.2化簡和式388

9.5.3次數的評估390

9.6圖書室391

9.6.1獨立與互斥391

9.6.2精確的評估392

9.6.3斯特林公式396

9.7回家路上403

9.8家405

第10章隨機算灋407

10.1休閒餐廳407

10.2學校409

10.2.1中午409

10.2.2快速排序算灋410

10.2.3通過樞紐項劃分數列—兩隻翅膀413

10.2.4對子數列排序—遞迴417

10.2.5運行步數的分析418

10.2.6分情况討論421

10.2.7最大運行步數425

10.2.8平均運行步數429

10.2.9回家路上434

10.3自己家435

10.3.1變形435

10.3.2 Hn與log n 441

10.4圖書室443

10.4.1米爾嘉443

10.4.2隨機快速排序444

10.4.3觀察比較過程447

10.4.4期望的線性法則452

10.4.5指示器隨機變數的期望等於概率453

10.5休閒餐廳456

10.5.1各種各樣的隨機算灋456

10.5.2準備457

10.6雙倉圖書館458

10.6.1 Iodine 458

10.6.2緊張459

10.6.3報告461

10.6.4傳達462

10.6.5 Oxygen 464

10.6.6連接465

10.6.7庭園466

10.6.8約定的印記468

尾聲471

後記477

參考文獻和導讀481